《1.2 数轴、相反数和绝对值》提升训练
1. 一个数在数轴上所对应的点向右移动5个单位长度后得到它的相反数的对应点,则这个数是.
A.-2 B.2 C.![]() D.
D.![]()
2. 若|x|=|y|,则x与y的关系是.
A.都是0 B.互为相反数 C.相等 D.相等或互为相反数
3. 若|a-1|+|b-2|=0,则a、b的值分别为.
A.1、2 B.-1、2 C.1、-2 D.-1、-2
4. 在-,-|-2|,-|4-4|,|-4|这四个数中,负数的个数有.
A.4个 B.3个 C.2个 D.1个
5. 已知|a|=2,|b|=1,|c|=3,且有理数a,b,c在数轴上的地方如图①所示,则a、b、c的值分别为.
![]()
图①
A.2,-1,3 B.-2,1,3 C.-2,-1,-3 D.2,1,-3
6. 如图②,数轴的单位长度为1,假如点A,B表示的数的绝对值相等,那样点A表示的数是.
![]()
图②
A.-4 B.-2 C.0 D.4
7. 假如|-a|=-a,那样.
A.-a肯定是负数 B.-a肯定是非负数
C.|-a|肯定是正数 D.|-a|肯定不是0
8. 在数轴上有两点,它们到表示-3的点的距离都等于4,那样这两个点表示的数是______.
9. 分别用数轴把下列各数表示出来,并求它们的相反数.
2,-1,0,1,-2,0.5.
10. 在正式的乒乓球比赛中,球的水平有严格的规定,下面是4个乒乓球的水平测试结果:-0.2,+0.3,-0.3,+0.15. 请指出什么乒乓球的水平好一些,并说明理由.
答案和分析
【答案】
1. D 2. D 3. A 4. D 5. B 6. B 7. B
8. 1和-7 9. 见答案 10. 最后一个球的水平最好
【分析】
1. 解:这对相反数在数轴上表示的点的距离为5,所以这两个数分别为![]() 与
与![]() ,
,
由题意知这个数为![]() .
.
故选D.
由题意可知,这对相反数在数轴上表示的点的距离为5,所以这两个数分别为![]() 与
与![]() ,进而可以得知这个数是多少.
,进而可以得知这个数是多少.
此题考查的是对数轴和相反数的认识,解题重点是剖析出在数轴上距离为5的这对相反数分别是多少.
2. 解:由于绝对值具备非负性,所以x,y的关系是相等或互为相反数.
故选D.
当x,y的关系是相等或互为相反数时,它们的绝对值相等.
此题考查的是绝对值的非负性,解题重点是理解绝对值的非负性,x,y的关系是相等或互为相反数,它们的绝对值相等.
3. 解:因为绝对值肯定是一个非负数,所以a-1=0,b-2=0.
所以a=1,b=2.
故选A.
依据绝对值的非负性可知,a-1=0,b-2=0,进而可以求出a、b的值.
此题考查的是对绝对值的认识,解题重点是明确绝对值的非负性.
4. 解:-=8,-|-2|=-2,-|4-4|=0,|-4|=4,
故负数有1个,
故选D.
要判断负数的个数,要化简后再察看结果.
此题考查的是相反数和绝对值的运算,解题重点是先化简再依据结果进行判断.
5. 解:由于|a|=2,|b|=1,|c|=3,所以a=±2,b=±1,c=±3,
结合数轴可知,a=-2,b=1,c=3.
故选B.
依据绝对值的概念可知,a=±2,b=±1,c=±3,再结合数轴即可得到a、b、c的值.
此题考查的是对数轴和绝对值的认识,解题重点是理解绝对值的概念,借助数轴得出a、b、c的值.
6. 解:点A、B在数轴上表示的点的距离为4,所以点A、B表示的数分别为2与-2,
结合数轴可知,点A表示的数是-2.
故选B.
由数轴可知,点A、B在数轴上表示的点的距离为4,所以点A、B表示的数分别为2与-2,
进而可以得知点A表示的数是多少.
此题考查的是对数轴和绝对值的认识,解题重点是剖析出点A、B在数轴上表示的点的距离为4.
7. 解:依据绝对值的非负性可知,
假如|-a|=-a,那样-a≥0,即-a肯定是非负数.
应选B.
一个正数的绝对值是它本身,0的绝对值是0,由|-a|=-a可知,-a≥0,从而可以选出正确的选项.
此题考查的是对绝对值的认识,解题重点是熟练学会绝对值的非负性.
8. 解:在数轴上有两点,它们到表示-3的点的距离都等于4,则这两点在表示-3的点的两侧,从表示-3的点开始分别向左和向右移动4个单位长度,那样这两个点表示的数是1和-7.
故答案为1和-7.
到表示-3的点的距离都等于4的两点在表示-3的点的两侧,从表示-3的点开始分别向左和向右移动4个单位长度,然后确定这两个点所表示的数即可.
此题考查的是对数轴的认识,解题重点是借用数轴剖析出两点的地方.
9. 解:把2,-1,0,1,-2,0.5用数轴表示为
![]()
2的相反数是-2;-1的相反数是1;0的相反数是0;1的相反数是-1;-2的相反数是2;0.5的相反数是-0.5.
在数轴上表示一些数时,应依据实质状况,灵活选取单位长度,本题中单位长度为1. 然后求出每个数的相反数即可.
此题考查的是数轴的画法及相反数的运算,解题重点是学会画数轴的步骤:画直线;定原点;选正方向;统一单位长度.
10. 解:由于|-0.2|=0.2,|+0.3|=0.3,|-0.3|=0.3,|+0.15|=0.15,0.3>0.2>0.15,
所以最后一个球的水平最好.
球的水平与标准水平越接近,球的水平越好.即看这四个数的绝对值,绝对值越小,越接近标准.
此题考查的是绝对值的实质应用,解题重点是要明确球的水平与标准水平越接近,球的水平越好.
《1.2 数轴、相反数和绝对值》培优训练
1. 已知有理数a,b,c满足|a-1|+|b-3|+|c-4|=0,则a,b,c的值分别为.
A.1,-3,4 B.-1,3,4 C.-1,-3,-4 D.1,3,4
2. 假如|m|=6,m的相反数是小于0的数,则|m-4|=.
A. -2 B. 2 C. 10 D. -10
3. 某汽配厂生产一批圆形的橡胶垫,从中抽取6件进行检验,比标准直径长的毫米数记作正数,比标准直径短的毫米数记作负数,检查结果如下:
1 | 2 | 3 | 4 |
+0.5 | -0.3 | +0.1 | 0 |
则水平最好的零件是.
A.第1个 B. 第2个 C. 第3个 D. 第4个
4. 一探险队,要沿着一条东西走向的河流进行考察,第一天沿河岸向上游走了5 km,第二天又向上游走了4.3 km,第三天开始计划有变,第三天又向下游走了4.8 km,第四天又向下游走了3 km,你了解第四天之后,该探险队在出发点的上游还是下游吗?距离出发点多远?
5. a,b,c三个数在数轴上的地方如图所示,化简式子:![]() .
.
![]()
答案和分析
【答案】
1. D 2. B 3. D
4. 探险队在出发点的上游,距离出发点1.5 km. 5. 1.
【分析】
1. 解:由于|a-1|≥0,|b-3|≥0,|c-4|≥0,且|a-1|+|b-3|+|c-4|=0,
所以|a-1|=0,|b-3|=0,且|c-4|=0.
所以a=1,b=3,c=4.
应选D.
依据绝对值的非负性,由|a-1|+|b-3|+|c-4|=0可知,|a-1|=0,|b-3|=0,|c-4|=0,进而可以求出a、b、c的值.
此题考查的是绝对值的非负性,任意一个数的绝对值都大于等于0,解题重点是由绝对值的非负性剖析出|a-1|=0,|b-3|=0,|c-4|=0.
2. 解:由于m的相反数是小于0的数,所以m大于0,
又由于|m|=6,所以m=6,
所以|m-4|=|6-4|=2.
故选B.
依据m的相反数是小于0的数可知,m大于0,进而可以得到m的值,最后求出|m-4|的值即可.
此题考查的是对相反数和绝对值的理解,解题重点是学会相反数和绝对值的概念.
3. 解:由于|+0.5|=0.5,|-0.3|=0.3, |+0.1|=0.1,|0|=0,0.5>0.3>0.1>0,
所以第4个零件的水平最好.
故选D.
水平的好坏取决于水平偏离标准水平的绝对数值,即偏离标准水平的数值越小越好.
此题考查的是绝对值的实质应用,解题重点是要明确偏离标准水平的数值越小,零件的水平越好.
4. 解:设出发点为原点,向上游走为正方向,那样向下游走为负,画出数轴如图所示.
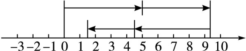
借助数轴剖析,得第四天后,探险队在出发点的上游,距离出发点1.5 km.
依据题意,规定正方向,画出数轴,然后借用数轴进行剖析即可.
本题主要考查了数轴的应用,解题重点是结合题意,借用数轴,画出探险队的运动轨迹.
5. 解:察看数轴上a,b,c的地方知:a是正数,b是正数,c是负数,
因此|a|=a,|b|=b,|c|=-c,
则![]() .
.
察看数轴可知,a是正数,b是正数,c是负数,进而可以得到|a|=a,|b|=b,|c|=-c,代入求出![]() 的值即可.
的值即可.
本题考查的是对数轴和绝对值的应用,解此题的重点是结合数轴可知a是正数,b是正数,c是负数,进而可以确定![]() ,
,![]() ,
,![]() 的值.
的值.







